Syntax Potential

Fawcett (2010: 172):

The main topic of this chapter will be the theory of syntax potential that is required in a modern SF grammar. I first used this term in Section 3.3 of Chapter 3 and it is modelled, as will be clear, on Halliday's characterisation of the system networks of TRANSITIVITY, MOOD, THEME and the rest as meaning potential. In Figure 4 we contrasted the 'meaning potential' of the grammar with its 'form potential', and 'syntax potential' is simply one part of the form potential.

Blogger Comments:

[1] This is misleading on several counts. Firstly, it is inconsistent with Halliday's notion of meaning potential, since Halliday models meaning potential as system, whereas Fawcett models syntax potential as realisation rules. Secondly, Halliday's notion of meaning potential refers to language as system, not just to the stratum of semantics (Fawcett's level of meaning). Thirdly, because Fawcett misunderstands 'meaning potential' to mean semantic systems, he gives here the false impression that Halliday characterises his own grammatical systems as semantic.

[2] Reminder:

To be clear, as previously explained, Fawcett's Figure 4 presents 

• form potential as realisation rules that involve meaning features,
• realisation rules (form) as the realisation of a system network (meaning), and
• structure as an instance of realisation rules.

Misunderstanding Instantiation

Fawcett (2010: 172):

As we saw in Chapter 3 — and most clearly in Figure 4 in Section 3.2 of that chapter — any adequate theory of language must provide, for each level of language, for both the potential and the instances of that potential. In some theories of language, of course, it is assumed that it is precisely the task of the theory of the potential (the grammar) to specify the instances that can be generated from the potential (the sentences of the language). But I have argued — both in Section 6.5 of Chapter 6 and more fully in Fawcett (1994a) — that, if we want a theory that can be used for modelling both the understanding and the generation of language texts, we need to recognise that we require a different set of concepts when faced with the task of analysing an incoming string of words (i.e., parsing) from those that are needed when we are trying to model the grammar in use for generation. In the process of generation there is no equivalent of the problematical task of parsing, as is demonstrated in Fawcett (1994a).

Blogger Comments:

[1] Reminder:

To be clear, Fawcett's model misconstrues instantiation as a relation between system and selection expression, at the level of meaning, and a relation between realisation rules and structure, at the level of form. As explained in many previous posts, a selection expression can be viewed as potential or instance, as shown by the phonological selection expression [voiced, bilabial, stop], which is synthetically realised by the phoneme /b/, whether as potential or as instance. As also explained in many previous posts, the relation between realisation rules and structure is the relation between the paradigmatic and syntagmatic axes: realisation, not instantiation.

[2] To be clear, both the grammar and 'the sentences of language' can be viewed as potential or instance. For example, 'the sentences of language' can be viewed as potential (grammatical systems) or as instances (in texts). It appears that Fawcett misunderstands 'instance' to simply mean 'output'.

[3] To be clear, in SFL Theory, the system is both the means by which speakers make meaning and the means by which addressees understand it. The different requirements of text generation and text parsing derive from trying to accommodate the fact that computers are not humans. A theory of language models the language of humans; a model of text generation and parsing by computers is not a model of human language.

"The Role Of 'Some Proposals' In Developing A Modern SF Theory Of Syntax"

Fawcett (2010: 166-7):

Let me now summarise this short chapter. "Some proposals" began the work of overhauling the concepts first presented in "Categories" in the light of the requirements of a modern theory of SF syntax — a theory in which the system networks of TRANSITIVITY, MOOD, THEME and the rest are regarded as modelling the level of meaning. As I wrote at the time, "the syntactic categories [...] are those [...] needed to state with the greatest economy the realisation rules that express the options in the semantics" (Fawcett 1974:4-5). The new ideas that it introduced have all proved their value, both in the construction of computer parsing systems (Weerasinghe & Fawcett 1993, Weerasinghe 1994 and Souter 1996) and in the hand analysis of texts by myself, my teaching colleagues, members of a large team of researchers in a study of the language of children aged 6-12, and many generations of students. 

However, later work has shown that in some cases the revisions were not drastic enough (e.g., the retention of the concept of the 'rank scale'). Yet in most cases the concepts established in "Some proposals" have passed the test of twenty-five years of use in various fields of application as a descr[ip]tion of English, as well as in describing various other languages, and they are the central concepts in the theory of syntax for a modern systemic functional grammar that I shall present in Part 2.

Blogger Comments:

[1] To be clear, Fawcett's "Some proposals" addressed Halliday's first theory, Scale and Category Grammar, after Halliday had devised his second theory, Systemic Functional Grammar, in the light of the requirements of a theory of syntax, despite the fact that neither of Halliday's theories is a theory of syntax, as previously explained.

[2] To be clear, in SFL Theory, the system networks of TRANSITIVITY, MOOD, THEME are located at the level of wording (lexicogrammar), not meaning (semantics). As Halliday (1985: xvii) explains:

The relation between meaning and wording is not, however, an arbitrary one; the form of the grammar relates naturally to the meanings that are being encoded. A functional grammar is designed to bring this out; it is a study of wording, but one that interprets the wording by reference to what it means.

[3] To be clear, this is a statement about Fawcett's model only (Figure 4), where realisation rules involving features of meaning are construed as the form that realises systems of meaning.

[4] To be clear, here Fawcett positively assesses his own model.

[5] To be clear, in SFL Theory, the rank scale is the means of modelling what other theories model as syntax.

Fawcett's Two Types Of Sequential Relationship And Recursion

Fawcett (2010: 166):

Two types of sequential relationship between sister elements of structure are recognised in "Some proposals": the segmental relationship of adjacency and the discontinuous relationship that occurs when elements are non-adjacent. These are not explicitly mentioned in "Categories", but every theory of syntax must have adequate ways of handling the various types of discontinuity found in language. Part 2 will introduce these concepts in Section 11.7 of Chapter 11.

Finally, two types of recursion are recognised. The first is embedding, in which a unit is 'rankshifted' (to use Halliday's original term) to fill an element of structure in a unit of the same or a lower rank. The second is co-ordination, in which two or more units fill a single element of structure.

With the exception of the concept of 'rank' — and so the derived concept of 'rank shift' — all of these 'relationships' are retained in the model of syntax to be presented in Part 2, and a small number of additional concepts that are not included in "Some proposals" are added to them. There is no need, therefore, to discuss the concepts of "Some proposals" any further at this point.

Blogger Comments:

[1] To be clear, SFL Theory proposes different structural relations for each metafunction, with 'segmental' describing experiential structures only. Halliday & Matthiessen (2014: 85):

[2] As previously noted, Fawcett's "Some proposals" (1974) was oriented to Halliday's first theory, Scale and Category Grammar, after it had been superseded by Halliday's second theory, Systemic Functional Grammar.

[3] To be clear, in formal theories, unlike SFL Theory, the term 'embedded' covers both rankshift and hypotaxis. Halliday & Matthiessen (2014: 382):

Such items are said to be ‘rankshifted’ – by contrast with ranking ones, which function prototypically as constituents of the higher unit. We may also use the term ‘embedded’, taken from formal grammars; but with the proviso that this term is often used to cover both rankshift (where the item is downgraded as a constituent) and hypotaxis (where the item is dependent on another one but is not a constituent of it. Here we shall use embedded only as an alternative term synonymous with rankshifted.

As will eventually be seen, Fawcett uses 'embedding' to include hypotactic relations between ranking clauses.

[4] To be clear, in SFL Theory, the traditional notion of co-ordination is treated as paratactic extension. Halliday & Matthiessen (2014: 472).

The combination of extension with parataxis yields what is known as co-ordination between clauses. It is typically expressed by and, nor, or, but.

Fawcett (p272), on the other hand, uses co-ordination and embedding to replace parataxis and hypotaxis, depending on the logico-semantic relation involved:

we treat four of Halliday's five types of 'hypotaxis' and two of his five types of 'parataxis' as embedding, and one type of 'hypotaxis' and his three 'expansion' types of 'parataxis' as co-ordination.

The problems with this approach will be identified when Fawcett's model is finally presented.

[5] To be clear, rank is the means by which SFL Theory models the phenomena of language known in other models as 'syntax'.

[6] To be clear, Fawcett's model includes embedding, but not rank-shift.

The Concept Of Rank In Fawcett's Models

Fawcett (2010: 165-6):

The concept of rank from "Categories" is retained in "Some proposals" — at least in relation to the clause and the group, which form the core of the model of syntax in all SFL descriptions (with far less work on the proposed 'morpheme-word' relationship). However, this small syntactic 'rank scale' is interpreted in a very different way from "Categories", because it is seen as the realisation of an equivalent semantic relationship between a 'situation' and the 'things' and 'qualities' that are its 'elements' at that higher level. And, as we shall see in Part 2, later work in this version of the theory was to reduce the role of the concept of a 'rank scale' to the point where it no longer has any status in the theory at all. … In the theory of syntax to be presented in Part 2 the concept of the 'rank scale' is replaced by the concept of probabilities in the relations between elements and units.

Blogger Comments:

[1] As previously noted, Fawcett's "Some proposals" (1974) was oriented to Halliday's first theory, Scale and Category Grammar, after it had been superseded by Halliday's second theory, Systemic Functional Grammar.

[2] This is potentially misleading, because SFL is not a theory of syntax. Halliday (1985: xiv):

[3] To be clear, this aspect of Fawcett's model is included in his Figure 12 (p210):

In SFL Theory, the semantic unit congruently realised by a clause depends on metafunction:

• figure (ideational)
• proposition/proposal (interpersonal)
• message (textual)

and ideationally, the semantic unit congruently realised by a group is an element (Halliday & Matthiessen 1999).

[4] To be clear, SFL Theory it is the rank scale that models the linguistic phenomena deemed 'syntax' in other theories.

[5] To be clear, in SFL Theory, rank is the ordering principle of structure (syntagmatic order), whereas probability is the quantification of system (paradigmatic order). This will be elaborated further in the examination of Fawcett's model in Part 2.

Fawcett's Componence, Filling and Exponence

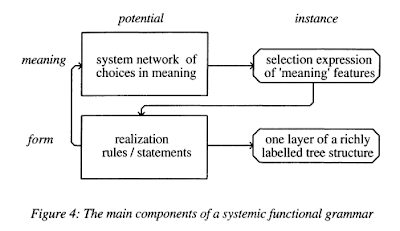
Fawcett (2010: 165):

8.4 The 'relationships' of "Some proposals" 

The first difference is that "Some proposals" recognises many more 'relationships' than the three 'scales' in "Categories". There are ten of them. 

One of its major innovations is to split Halliday's 'scale' of 'exponence' into three: componence, filling and exponence proper. To cite Butler's excellent summary of these concepts:

Componence is the relation between a unit and the elements of structure of which it is composed. For example, a clause may be composed of the elements S, P, C and A. Each of these elements of structure may be (but need not be) filled by groups. In the specification of a syntactic structure, componence and filling alternate until, at the bottom of the structural tree, the smallest elements of structure are not filled by other units. It is at this point that we need the concept of exponence, as used by Fawcett: the lowest elements of structure are expounded by items', which are [...] more or less equivalent to 'words' and 'morphemes' in Halliday's model. (Butler 1985:95) 

These three concepts, which today still form the basis of the Cardiff Grammar's model of syntax, are clearly exemplified in the top half of Figure 10. These concepts are necessary, in one form or another, in any adequate systemic functional model of syntax, and they will be illustrated, discussed and compared with their antecedents in the relevant sections of Chapter 11.

Blogger Comments:

[1] As previously noted, Fawcett's "Some proposals" (1974) was oriented to Halliday's first theory, Scale and Category Grammar, after it had been superseded by Halliday's second theory, Systemic Functional Grammar.

[2] To be clear, in Halliday's first theory, the term 'exponence' covered what were to become two distinct relations in his second theory: realisation and instantiation. On the one hand, exponence corresponds to the relation between an element of function structure and the class of unit that realises it. Halliday (2002 [1961]: 54, 57):

The exponent of the element S in primary clause structure is the primary class nominal of the unit group. …

The fact that by moving from structure to class, which is (or can be) a move on the exponence scale, one also moves one step down the rank scale, is due to the specific relation between the categories of class and structure, and not to any inherent interdetermination between exponence and rank.

On the other hand, exponence corresponds to the instantiation relation between theory and data. Halliday (2002 [1961]: 57):

Exponence is the scale which relates the categories of the theory, which are categories of the highest degree of abstraction, to the data.

[3] To be clear, 'componence' is the relation of composition, a type of extension. In SFL Theory, composition is modelled as a rank scale of forms, and is distinct from the function structures of the units on the rank scale.

[4] To be clear, one the one hand, Fawcett's 'filling' corresponds to the relation between an element of clause structure and the group that realises it, but treats these two distinct levels of symbolic abstraction, function and form as if both were at the same level. On the other hand, 'filling' suggests an active process, rather than an inert relation, and if this were a model of human language, rather than an algorithm for text generation, the process would be (an aspect of) instantiation.

[5] To be clear, Fawcett's 'exponence' corresponds to the relation between an element of group structure and the word (and morphemes) that realise it. That is, it is a different term for the same relation as 'filling': realisation.

[6] This is misleading, because it is untrue. As can be seen below, while Figure 10 does exemplify Fawcett's notion of componence, a form (clause) composed of functions, it does not exemplify the filling of clause functions by groups or the exponence of groups by words and morphemes. (The 'text' line is the data being analysed, not an analysis of the data at group or word level.)

Systemic Syntax Without Systems

Fawcett (2010: 165):

The last of the three theoretical categories recognised in "Some proposals" (along with 'unit' and 'class of unit') was element of structure. Like 'unit', this term was used in essentially the same sense as in "Categories". However, the concept plays a far stronger part in the theory as a whole than it does in "Categories" because of the mutual dependency, in the present framework, of the definitions of a class of unit and its elements of structure. In "Categories", in contrast, a class of unit is defined by its potential for "operation in the structure of the unit next above" (1961/76:64).

In two of its 'categories', then, "Some proposals" is similar to Halliday (1961/76). While the concept of 'class of unit' is broadly similar, the criteria for recognising the 'class' of a 'unit' are very different, and the concept of 'system' does not appear at this level of description at all. However, there are even greater differences between the 'scales' of "Categories" and the 'relationships' of "Some proposals", as the next section shows.

Blogger Comments:

[1] As previously noted, Fawcett's "Some proposals" (1974) was oriented to Halliday's first theory, Scale and Category Grammar, after it had been superseded by Halliday's second theory, Systemic Functional Grammar.

[2] As previously explained, this downplaying of difference is misleading, because the difference between Fawcett's notion of 'class of unit' and Halliday's notion is indeed significant. Halliday (1961) takes the view 'from above', distinguishing classes of unit according to the functions they realise, whereas Fawcett takes the view 'from below', distinguishing classes of unit according to the structures that realise them. Halliday (2002 [1961]: 50):

What is theoretically determined is the relation between structure and class on the one hand and unit on the other. Class, like structure, is linked to unit: a class is always a class of (members of) a given unit: and the class–structure relation is constant – a class is always defined with reference to the structure of the unit next above, and structure with reference to classes of the unit next below. A class is not a grouping of members of a given unit which are alike in their own structure. In other words, by reference to the rank scale, classes are derived “from above” (or “downwards”) and not “from below” (or “upwards”).

Moreover, as the units 'quantity group', 'quality group' and 'tempering cluster' demonstrate, Fawcett confuses classes of units with their functions.

[3] To be clear, if the concept of system does not "appear" at the level of syntax, then Fawcett's claim that his model is a systemic model of syntax is invalid.

Classes Of 'Cluster' And No Classes Of 'Word'

Fawcett (2010: 164):

Three classes of the new unit of the cluster were tentatively recognised in the 1974-6 edition: the genitive cluster (e.g., her boyfriend's)', the proper name cluster (e.g., Dr Ivy Idle) and the tempering cluster (e.g., much less in much less painful). By 1981 the 'tempering cluster' had been absorbed into the 'quantity-quality group', and later still the data that it covers became part of the evidence for the need to introduce the 'quantity group'. Further classes of 'cluster' are added in the current version of the grammar, as described in Part 2.

There was no discussion in "Some proposals" of the concept of 'class of word', because 'words' are treated there as items rather than as syntactic units (1974-6/81:67). (See Part 2 for a fuller justification for taking the position that the relationship of morphemes to a word is not the same as that between, let us say, groups and clauses.)

Blogger Comments:

[1] To be clear, like the notions of 'quantity group' and quality group, the notion of a 'tempering cluster' mistakes a function of a cluster (tempering) for a class of a cluster.

[2] To be clear, in SFL Theory, 'word' is used for two distinct abstractions: lexical item and grammatical rank scale unit. The word as lexical item is the synthetic realisation of the most delicate lexicogrammatical features — just as the phoneme /b/ is the synthetic realisation of the features [voiced, bilabial, stop]. The word as grammatical unit is (i) a constituent of groups/phrases and realises elements of their function structures, and (ii) composed of morphemes. It is the word as grammatical unit that is differentiated by (grammatical) class.

[3] Fawcett's justification for his position will be critically evaluated in the examination of Part 2.

[4] To be clear, in SFL Theory, the relationship of morphemes to a grammatical word, and of groups to clauses is the same: constituency. It is this commonality that allows Halliday to model syntax and morphology as a rank scale in both theories, Scale and Category Grammar and Systemic Functional Grammar. For example, for Scale and Category Grammar, Halliday (2002 [1961]: 51) explains:

Traditionally these terms have usually referred to “grammar above the word” (syntax) and “grammar below the word” (morphology); but this distinction has no theoretical status. It has a place in the description of certain languages, “inflexional” languages which tend to display one kind of grammatical relation above the word (“free” items predominating) and another below the word (“bound” items predominating). But it seems worthwhile making use of “syntax” and “morphology” in the theory, to refer to direction on the rank scale. “Syntax” is then the downward relation, “morphology” the upward one; and both go all the way. We can then say, simply, classes are syntactical and not morphological.

Later Changes (1981) To Fawcett's "Some Proposals" (1974): Verbal, Quality & Quantity Groups

Fawcett (2010: 164):

However, by the 1981 edition I had made several changes to the model. Firstly, I had strengthened my position on the supposed 'verbal group', writing that even for text analysis the elements of the supposed 'verbal group' "would in my view be best shown as clause elements" (Fawcett 1974-6/81:31) (See Fawcett (2000) and (forthcoming b) for the full set of reasons and Appendix C for a summary of them.) Secondly the 'adjectival' and 'adverbial' groups, which were already shown in the 1974-6 edition as sharing a common structure, were brought together as the 'quantity-quality group' (since they typically express the meaning of a 'quantity' of a 'quality'). And thirdly the 'prepend group' had been re-named the "prepositional group". Later still, as Part 2 shows, I realised that, in order to provide an adequate description of English and other languages, we need to recognise both a quality group and a quantity group. See Tucker (1998) for the fullest explanation of the quality group in English and Fawcett (in press) for an introduction to both classes of group.

 Blogger Comments:

[1] As will be seen in the examination of Appendix C, Fawcett's argument against the verbal group (pp333-6) centres on misunderstandings involving the Finite element and phrasal verbs.

[2] To be clear, the notion of 'quality group' and 'quantity group' confuses class (of group) with function (of group).

[3] As previously noted, Fawcett (in press) is still unpublished, 20 years after the first edition of this work.

The Concepts Of Unit And Class Of Unit In Fawcett's "Some Proposals" (1974)

Fawcett (2010: 163-4):

"Some proposals" recognises a number of units (in precisely the same sense of "unit" as in "Categories"). These units are related to each other on a 'rank scale', and for English they are: clause, group and cluster. The unit 'cluster' is a new unit that is lower on the 'rank scale' than the group; see below for examples. (The concept of 'unit', which is mutually defining with that of the 'rank scale', is not used in the framework to be proposed in Part 2.)

"Some proposals" uses the concept of class of unit in a way that is loosely similar to its use in "Categories". It relates the concept of 'class of unit' to 'unit' essentially as in "Categories", except that the criteria for recognising a given class of unit are the elements of its internal structure, rather than its potential for operation in the unit above, as in "Categories". (For a full discussion of the criteria for recognising classes of unit, see Section 10.2.2 of Chapter 10.) On this criterion, "Some proposals" recognises only classes of groups and clusters (and not clauses or words). Thus it recognises that, at the 'rank' of clause rank in English, there is only one 'class' of clause, so that the concept of 'class of unit' is not applicable to this unit. At group rank "Some proposals" initially recognised four classes. These were the nominal group (e.g., she, Ivy and the man in black), the prepend group (e.g., in black), the adjectival group (e.g., very quick) and the adverbial group (e.g., very quickly). In the 1974-6 edition I further suggested (1974-6/81:31) that "in an introductory analysis it is probably helpful to make use of the traditional S&C concept of the 'verbal group'"(e.g., might have seen).

Blogger Comments:

[1] To be clear, Fawcett's "Some proposals" (1974) was oriented to Halliday's first theory, Scale and Category Grammar, after it had been superseded by Halliday's second theory, Systemic Functional Grammar.

[2] This downplaying of difference is misleading, because the difference between Fawcett's notion of 'class of unit' and Halliday's notion is indeed significant. Halliday (1961) takes the view 'from above', distinguishing classes of unit according to the functions they realise, whereas Fawcett takes the view 'from below', distinguishing classes of unit according to the structures that realise them. Halliday (2002 [1961]: 50):

What is theoretically determined is the relation between structure and class on the one hand and unit on the other. Class, like structure, is linked to unit: a class is always a class of (members of) a given unit: and the class–structure relation is constant – a class is always defined with reference to the structure of the unit next above, and structure with reference to classes of the unit next below. A class is not a grouping of members of a given unit which are alike in their own structure. In other words, by reference to the rank scale, classes are derived “from above” (or “downwards”) and not “from below” (or “upwards”).

[3] To be clear, Fawcett's "Some proposals" (1974) does not recognise classes of words: nouns, adjectives, verbs, adverbs, prepositions, conjunctions.

[4] To be clear, although not acknowledged, this is also the case in Halliday (1961).

The Other Types Of 'Form' In Fawcett's "Some Proposals" (1974)

Fawcett (2010: 163):

"Some proposals" was written as a short description of the syntax of English, and it concludes with a summary of the theory that the description presupposed. The structure of the paper therefore reflects the view that theory should grow out of description — or, more accurately, out of the attempt to apply the concepts of an earlier theory (here "Categories") in a description. In my view, this interleaving of theory and description is one of the more effective ways to improve one's theory — as well as through the use of corpora and, as suggested in Section 1.2 of Chapter 1, large scale computer implementations. (See also the discussion of the relationships between theory, description and application in Halliday & Fawcett 1987b:1f.).

We must begin by relating the model of syntax to the model of language as a whole. Within a model of the sort presented in Figure 4 in Section 3.2 of Chapter 3, "Some proposals" sees syntax as one of three ways in which meanings are realised as forms — the other types of 'form' being items and intonation or punctuation (depending on the channel of discourse).

Blogger Comments:

[1] To be clear, Fawcett's "Some proposals" (1974) presupposed Halliday's first theory, Scale and Category Grammar, after it had been superseded by Halliday's second theory, Systemic Functional Grammar.

[2] To be clear, a linguistic theory is a model of language, and a linguistic description is the application of a theory to a particular language. For example, Halliday's IFG (1985, 1994) presents a theory of language which is applied to a description of English. That is, theory precedes description, and the description of data tests the theory that is designed to account for the data.

[3] To be clear, computer implementations of a theory, large or small, are concerned with adapting a theory of language to the limitations of machines. This is distinct from modelling language as a system that has evolved in the human species.

[4] Reminder:

[5] To be clear, Fawcett's "Some proposals" (1974) locates some aspects of the content plane — syntax and items (words and morphemes) — and some aspects of the expression plane — intonation or punctuation — at the same level of symbolic abstraction: form.

The omissions in these characterisations of phonology (rhythm and articulation) and graphology (orthography) will be examined when Fawcett eventually discloses his current model. For the moment, it can be seen, from Figure 4, where system networks are limited to his level of meaning, that Fawcett does not model phonology and graphology as systems.

"My Theory Of Syntax"

Fawcett (2010: 162-3):

The following words provide the key to understanding my original motivation for developing a framework for representing structure — a framework that was very different from the 'multiple structure' model that Halliday was developing at about the same time:

the syntactic categories [...] are those [...] needed to state with the greatest economy the realisation rules that express the options in the semantics (Fawcett 1974:4-5). 

Over twenty-five years later, my theory of syntax and the consequent description of English syntax have both developed in various ways, but those words still express exactly what I wish to say on this matter. It is because the description of the functional structure is necessarily complemented, in my approach, by a description in terms of a functional semantics that the syntax can — and should — be less "extravagant" (Halliday 1994:xix) than it is in Halliday's IFG. Moreover, I have discovered in the intervening time that this general principle holds just as strongly for the version of the grammar that is used for the computer model of natural language generation as it does for the version used for text analysis. The clear implication of all of this work is that we cannot provide a complete description of a text without providing both an analysis of its functional syntax and an account of the semantic features that have been chosen in generating it. 

Blogger Comments:

[1] To be clear, this is a statement that only applies to Fawcett's own model (Figure 4), in which structure is misunderstood as an "instance" of realisation rules which are, in turn, misunderstood as the form that realises systems. Both of Halliday's theories model syntax as a compositional rank scale on the stratum of lexicogrammar. As will be seen, Fawcett rejects the theoretical value of a rank scale.

[2] To be clear, as previously explained, Fawcett's syntax is only "less extravagant" than Halliday's function structures because Fawcett exports the majority of Halliday's grammatical functions to his level of meaning. When these exported functions are counted in the description, Fawcett's "less extravagant" model of the clause involves at least seven lines of description (Figure 10), compared with Halliday's "more extravagant" three (theme, mood, transitivity).

[3] To be clear, this is a personal recount presented as if reasoned argumentation.

[4] To be clear, this is again a statement of Fawcett's model, not Halliday's Systemic Functional Grammar. In Systemic Functional Grammar, there is no "functional syntax", and what Fawcett terms 'semantic features' are features of lexicogrammatical systems. In the absence of grammatical metaphor, lexicogrammatical features are congruent with (agree with) semantic features. It is grammatical metaphor that motivates the distinction between semantic and lexicogrammatical systems.

A Second Motivation For Fawcett's "Some Proposals" (1974)

Fawcett (2010: 162):

There was a second motivation, however. This was that my attempts to apply Halliday's categories in the analysis of text at the level of form had led me to modify his description in a number of ways — and so in due course to think about the consequences of these descriptive changes for the theory upon which the description rested.

Blogger Comments:

[1] To be clear, neither Halliday's first theory, Scale and Category Grammar, nor his second, Systemic Functional Grammar, postulates a level of form. The fact that Fawcett attempted to apply Halliday's categories at "the level of form" demonstrates that Fawcett did not understand either of Halliday's theories, and that his modifications to Halliday's "descriptions"  — and their consequences — derive from his inability to understand them.

[2] To be clear, as Fawcett acknowledges (p161) his "Some Proposals" (1974) presented his set of revisions to the concepts of "Categories", an outline of Halliday's first theory, Scale and Category Grammar, after Halliday had already devised an early version of his second theory, Systemic Functional Grammar. Scale and Category Grammar is not the theory on which Systemic Functional Grammatical descriptions rested.